Algorithm/백준
[백준 / 2342 / Python] Dance Dance Revolution
Kun Woo Kim
2025. 6. 13. 22:17
728x90
반응형
문제 요약
DDR(Dance Dance Revolution) 게임에서,
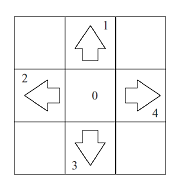
중앙(0)과 네 방향(1: 위, 2: 왼쪽, 3: 아래, 4: 오른쪽) 발판이 있습니다.
처음엔 두 발 모두 중앙(0)에 있고, 주어진 스텝 순서대로 한 발씩 움직여야 합니다.
- 같은 위치에 두 발이 동시에 있을 수는 없습니다(시작 제외).
- 한 발이 이미 해당 위치에 있다면, 그 발로 반복해서 눌러야 합니다.
발을 움직일 때 드는 힘은 다음과 같습니다:
- 중앙(0) → 다른 위치: 2
- 같은 위치 반복: 1
- 인접한 위치로 이동: 3
- 반대편(예: 위↔아래, 왼↔오른) 이동: 4
모든 스텝을 밟는 데 필요한 최소 힘을 구하는 문제입니다.
접근 방식
이 문제는 "상태"를 잘 정의해서 DP(동적 프로그래밍)로 해결해야 합니다.
- 각 스텝마다, 왼발과 오른발이 각각 어디에 있는지(0~4), 그리고 몇 번째 스텝까지 밟았는지(i)를 상태로 둡니다.
- dp[i][l][r] = i번째 스텝까지 밟았을 때, 왼발이 l, 오른발이 r에 있을 때의 최소 힘
- 매 스텝마다, 왼발 또는 오른발을 움직이는 두 가지 경우를 모두 고려해,
각 경우의 힘을 계산하고, 더 작은 값을 갱신합니다.
실생활 비유로 설명하면,
"매번 왼발로 밟을지, 오른발로 밟을지 시뮬레이션하며,
가장 힘이 적게 드는 경로만 남겨두는 것"과 같습니다.
코드 구현
아래는 Python으로 구현한 코드입니다.
import sys
INF = sys.maxsize
input = sys.stdin.readline
steps = list(map(int, input().split()))
steps.pop() # 마지막 0 제거
n = len(steps)
adjacent = {
1: [2, 4],
2: [1, 3],
3: [2, 4],
4: [1, 3]
}
# from, to
def move_cost(f, t):
if f == 0:
return 2
elif f == t:
return 1
elif t in adjacent.get(f, []):
return 3
else:
return 4
dp = [[[INF] * 5 for _ in range(5)] for _ in range(n + 1)]
dp[0][0][0] = 0
for i in range(n):
current = steps[i]
for l in range(5):
for r in range(5):
if dp[i][l][r] == INF:
continue
# 왼발로 밟기
if current != r:
cost = move_cost(l, current)
dp[i + 1][current][r] = min(dp[i + 1][current][r], dp[i][l][r] + cost)
# 오른발로 밟기
if current != l:
cost = move_cost(r, current)
dp[i + 1][l][current] = min(dp[i + 1][l][current], dp[i][l][r] + cost)
answer = INF
for l in range(5):
for r in range(5):
answer = min(answer, dp[n][l][r])
print(answer)시간복잡도 & 최적화
- 시간복잡도:
- 스텝 수 n에 대해, 각 단계마다 왼발/오른발 위치(5×5) 상태를 모두 고려하므로
O(n × 5 × 5) = O(n) 수준 (n ≤ 100,000)
- 스텝 수 n에 대해, 각 단계마다 왼발/오른발 위치(5×5) 상태를 모두 고려하므로
- 최적화 포인트:
- 불가능한 상태는 INF로 두고, 실제로 도달 가능한 상태만 갱신
- move_cost 함수로 이동 비용을 일관성 있게 관리
느낀 점 / 팁
- "상태"를 잘 정의하면 복잡한 시뮬레이션 문제도 DP로 깔끔하게 풀 수 있습니다.
- 2차원 평면에서의 이동 비용 문제는,
인접/반대/같은 위치 등 조건을 함수로 분리하면 코드가 훨씬 명확해집니다. - DP 테이블이 커 보여도, 실제로는 도달 가능한 상태만 갱신하므로
메모리와 시간 모두 효율적으로 관리할 수 있습니다.
참고
728x90
반응형