Algorithm

"이 알고리즘이 더 빠른가요?" Big O 표기법으로 정확하게 답하는 법

Kun Woo Kim 2025. 11. 11. 10:49
728x90

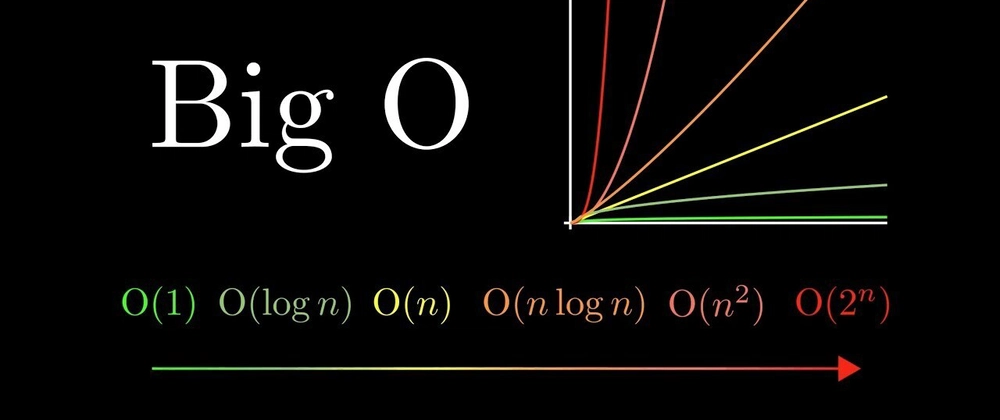
들어가며

"이 알고리즘이 더 빠른데?" vs "저 알고리즘이 더 빠른데?"

개발자들 사이에서 흔히 일어나는 논쟁입니다. 하지만 '빠르다'는 표현은 생각보다 애매합니다. 내 컴퓨터에서는 0.5초 걸렸는데, 동료 컴퓨터에서는 0.2초 걸렸다면? 과연 어느 알고리즘이 더 효율적인 걸까요?

이런 모호함을 해결하기 위해 컴퓨터 과학에서는 Big O 표기법이라는 표준화된 방법을 사용합니다. 오늘은 이 Big O 표기법을 통해 알고리즘의 성능을 제대로 평가하는 방법을 알아보겠습니다.

왜 시간이 아닌 단계(Step)로 측정할까?

알고리즘의 성능을 초 단위로 측정하지 않는 이유는 명확합니다. 같은 알고리즘이라도 하드웨어 성능에 따라 실행 시간이 달라지기 때문입니다.

  • 최신 M4 맥북에서 돌린 알고리즘: 0.1초
  • 10년 된 노트북에서 돌린 같은 알고리즘: 1초

이렇게 되면 알고리즘 자체의 효율성을 객관적으로 평가할 수 없습니다. 그래서 우리는 알고리즘이 수행하는 단계(step)의 수로 성능을 측정합니다.

예를 들어:

  • 5단계로 끝나는 알고리즘 A
  • 10단계로 끝나는 알고리즘 B

어떤 컴퓨터에서 실행하든 A가 B보다 효율적이라는 것은 변하지 않습니다.

Big O 표기법이란?

Big O 표기법은 입력 크기(n)에 따라 알고리즘이 몇 단계를 수행하는지를 표현하는 방법입니다.

예를 들어 선형 탐색(Linear Search) 알고리즘을 생각해봅시다:

  • 크기 10인 배열: 최악의 경우 10단계
  • 크기 20인 배열: 최악의 경우 20단계
  • 크기 n인 배열: 최악의 경우 n단계

이를 간단하게 O(n)이라고 표현합니다.

"입력 크기가 n일 때 n단계가 필요합니다"라는 긴 문장 대신, 단순히 "시간 복잡도가 O(n)입니다"라고 말할 수 있게 된 것이죠. 훨씬 깔끔하고 전문적이지 않나요?

주요 시간 복잡도 유형

1. O(1) - 상수 시간 (Constant Time)

def print_first_element(array):
    print(array[0])  # 1단계

입력 크기와 관계없이 항상 일정한 단계만 수행하는 알고리즘입니다.

  • 배열 크기가 10이든 100이든 1,000이든: 항상 1단계
  • 가장 이상적인 시간 복잡도

중요한 규칙: Big O는 상수를 무시합니다.

def print_first_element_twice(array):
    print(array[0])  # 1단계
    print(array[0])  # 1단계

위 함수는 기술적으로 2단계지만, O(2)가 아닌 O(1)로 표기합니다. Big O는 세부사항보다는 전체적인 경향성에 집중하기 때문입니다.

만약 어떤 함수가 항상 200단계를 수행한다 해도 O(200)이 아닌 O(1)입니다. 입력 크기가 증가해도 단계 수가 증가하지 않는다는 본질이 중요하기 때문이죠.

그래프로 보면 수평선처럼 평평한 모양입니다.

2. O(n) - 선형 시간 (Linear Time)

def print_all_elements(array):
    for element in array:
        print(element)

입력 크기에 비례하여 단계가 증가하는 알고리즘입니다.

  • 배열 크기가 10: 10단계
  • 배열 크기가 100: 100단계

여기서도 상수는 무시됩니다:

def print_all_elements_twice(array):
    for element in array:
        print(element)
    for element in array:
        print(element)

기술적으로는 O(2n)이지만, O(n)으로 표기합니다. 2배든 3배든 입력이 증가하면 단계도 선형적으로 증가한다는 본질은 같기 때문입니다.

그래프로 보면 대각선 모양의 직선입니다.

3. O(n²) - 이차 시간 (Quadratic Time)

def print_all_pairs(array):
    for element1 in array:
        for element2 in array:
            print(element1, element2)

중첩 반복문이 있을 때 주로 발생합니다.

  • 배열 크기가 10: 100단계 (10 × 10)
  • 배열 크기가 20: 400단계 (20 × 20)

입력이 2배 증가하면 실행 단계는 4배 증가합니다. 입력이 커질수록 급격하게 비효율적이 되는 전형적인 패턴이죠.

버블 정렬, 선택 정렬 같은 단순한 정렬 알고리즘들이 이런 시간 복잡도를 가집니다.

4. O(log n) - 로그 시간 (Logarithmic Time)

이진 탐색(Binary Search)처럼 데이터를 반씩 줄여나가는 알고리즘입니다.

로그(logarithm)를 간단히 복습하자면:

2⁵ = 32  →  log₂(32) = 5

"2를 몇 번 곱해야 32가 될까?" (답: 5번) 이것이 지수(exponent)고,
"32를 2로 몇 번 나눠야 1이 될까?" (답: 5번) 이것이 로그입니다.

이진 탐색에서는:

32개 요소 → 16개 → 8개 → 4개 → 2개 → 1개 (5단계)
64개 요소 → 32개 → 16개 → 8개 → 4개 → 2개 → 1개 (6단계)

입력이 2배 증가해도 단계는 1개만 증가합니다. 매우 효율적이죠!

Big O 표기법에서는 밑(base)을 생략하고 그냥 O(log n)으로 씁니다. 밑이 2든 10이든 전체적인 경향성은 같기 때문입니다.

그래프로 보면 처음에는 급격히 증가하다가 점점 완만해지는 곡선 모양입니다.

시간 복잡도 비교

효율성 순서로 나열하면:

  1. O(1) - 상수 시간 ⭐⭐⭐⭐⭐ (최고)
  2. O(log n) - 로그 시간 ⭐⭐⭐⭐
  3. O(n) - 선형 시간 ⭐⭐⭐
  4. O(n log n) - 선형 로그 시간 ⭐⭐
  5. O(n²) - 이차 시간 ⭐
  6. O(2ⁿ) - 지수 시간 💀 (최악)

실무에서는:

  • O(1), O(log n), O(n): 좋은 알고리즘
  • O(n log n): 합병 정렬, 퀵 정렬 등 실용적인 정렬 알고리즘
  • O(n²) 이상: 입력 크기가 작을 때만 사용 가능

실전 예제로 이해하기

배열의 첫 번째 요소 출력

function printFirst(arr: number[]): void {
    console.log(arr[0]);
}
// 시간 복잡도: O(1)

입력 크기와 무관하게 항상 1단계입니다.

배열의 모든 요소 출력

function printAll(arr: number[]): void {
    arr.forEach(item => console.log(item));
}
// 시간 복잡도: O(n)

배열 크기만큼 반복하므로 O(n)입니다.

이진 탐색

function binarySearch(sortedArr: number[], target: number): number {
    let left = 0;
    let right = sortedArr.length - 1;

    while (left <= right) {
        const mid = Math.floor((left + right) / 2);

        if (sortedArr[mid] === target) return mid;
        if (sortedArr[mid] < target) left = mid + 1;
        else right = mid - 1;
    }

    return -1;
}
// 시간 복잡도: O(log n)

매 단계마다 탐색 범위를 반으로 줄이므로 O(log n)입니다.

버블 정렬

function bubbleSort(arr: number[]): number[] {
    const n = arr.length;

    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
            }
        }
    }

    return arr;
}
// 시간 복잡도: O(n²)

중첩 반복문으로 인해 O(n²)입니다.

Big O 표기법의 실용적 가치

Big O 표기법을 이해하면:

  1. 알고리즘 선택: 상황에 맞는 최적의 알고리즘을 선택할 수 있습니다.
  2. 코드 리뷰: 동료의 코드에서 비효율적인 부분을 발견할 수 있습니다.
  3. 성능 예측: 사용자가 늘어났을 때 시스템이 어떻게 동작할지 예측 가능합니다.
  4. 기술 면접: 면접에서 알고리즘 문제를 풀 때 필수적인 개념입니다.

예를 들어 100개 요소를 처리하는 O(n²) 알고리즘은 10,000단계가 필요하지만, O(n log n) 알고리즘은 약 664단계만 필요합니다. 데이터가 많아질수록 이 차이는 더욱 극명해집니다.

주의사항

Big O는 최악의 경우(worst case)를 나타냅니다. 실제로는 더 빠르게 동작할 수 있지만, 보장할 수 있는 최악의 시나리오를 기준으로 평가합니다.

또한 Big O만으로 모든 것을 판단할 수는 없습니다:

  • 상수 계수가 클 수도 있습니다 (O(1)이지만 100만 단계일 수도)
  • 실제 메모리 사용량은 별개입니다
  • 입력이 작으면 O(n²)이 O(n log n)보다 빠를 수도 있습니다

마치며

Big O 표기법은 알고리즘의 효율성을 표현하는 표준 언어입니다. 처음에는 낯설 수 있지만, 익숙해지면 알고리즘을 평가하고 개선하는 데 강력한 도구가 됩니다.

다음번에 코드를 작성할 때, 한 번쯤 생각해보세요. "이 코드의 시간 복잡도는 얼마나 될까?" 이런 질문을 던지는 습관만으로도 더 나은 개발자가 될 수 있습니다.

728x90
저작자표시 비영리 변경금지 (새창열림)