머리글
2021 KAKAO BLIND RECRUITMENT의 합승 택시 요금을 풀면서 무지와 어피치가 합승을 할 수 있다는 점에 주목하여 플로이드-워셜 알고리즘을 사용했지만, 효율성 테스트에서 낮은 점수를 받았다. 이를 계기로 다익스트라 알고리즘과 플로이드-워셜의 차이를 다시 정리하고, 각 알고리즘의 적절한 사용 전략을 세울 필요성을 느꼈다.
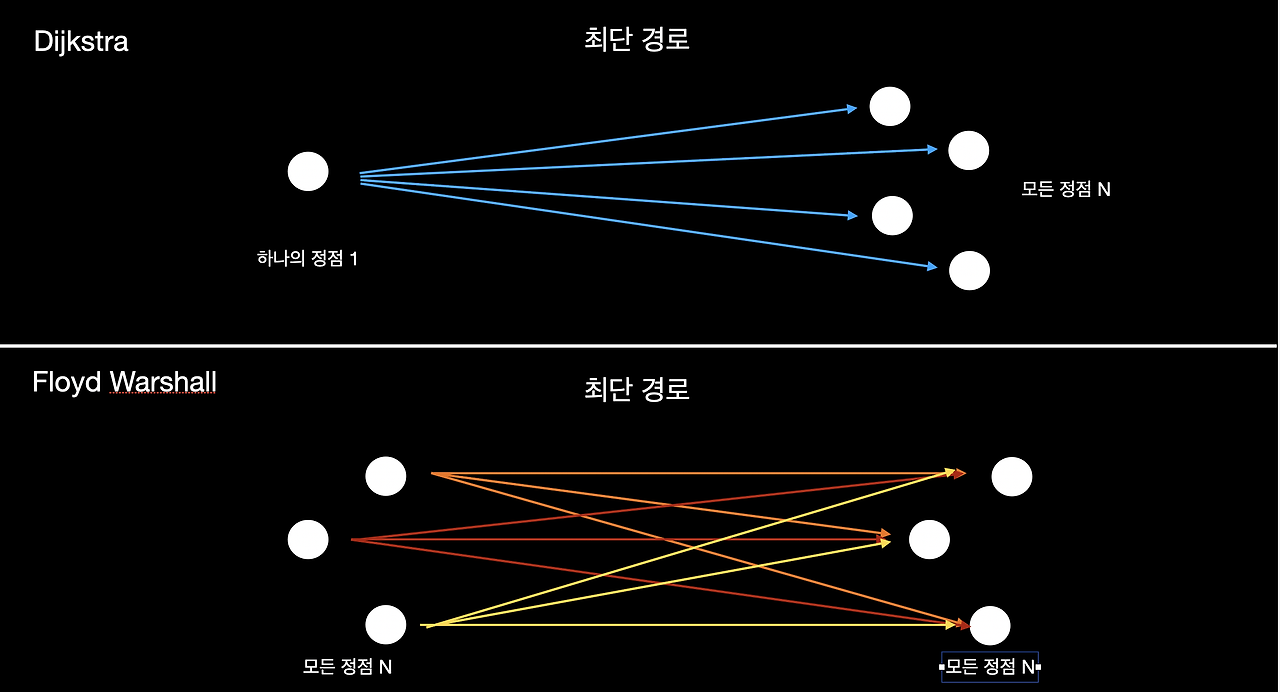
다익스트라(Dijkstra) 알고리즘은 하나의 정점에서 출발하여 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이고, 플로이드-워셜(Floyd-Warshal) 알고리즘은 모든 정점에서 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다.
Dijstra vs FloydWarshall
다익스트라(Dijkstra) 알고리즘
다익스트라 알고리즘은 하나의 시작 정점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이다. 이 알고리즘은 음의 가중치가 없는 그래프에서만 동작하며, 그리디 알고리즘의 일종으로 분류된다.
동작 과정:
시작 정점 설정: 시작 정점을 선택하고, 해당 정점의 최단 거리를 0으로 설정한다. 나머지 정점들의 최단 거리는 무한대로 초기화한다.
방문하지 않은 정점 중 최단 거리 선택: 현재 방문하지 않은 정점들 중에서 최단 거리가 가장 짧은 정점을 선택한다.
최단 거리 갱신: 선택된 정점을 거쳐 다른 인접한 정점으로 가는 거리를 계산하여, 기존의 최단 거리보다 짧으면 갱신한다.
반복: 모든 정점을 방문할 때까지 2번과 3번 과정을 반복한다.
구현 예시
import heapq
def dijkstra(graph, start):
# 시작 정점에서 각 정점까지의 최단 거리를 저장하는 딕셔너리
distances = {node: float('inf') for node in graph}
distances[start] = 0
# 우선순위 큐 (힙)
priority_queue = [(0, start)]
while priority_queue:
current_distance, current_node = heapq.heappop(priority_queue)
# 현재 노드가 이미 처리된 적이 있으면 무시
if current_distance > distances[current_node]:
continue
# 인접한 노드들에 대해 최단 거리 갱신
for adjacent, weight in graph[current_node].items():
distance = current_distance + weight
# 더 짧은 경로를 발견하면 갱신하고 우선순위 큐에 추가
if distance < distances[adjacent]:
distances[adjacent] = distance
heapq.heappush(priority_queue, (distance, adjacent))
return distances구현 예시
graph = {
'A': {'B': 2, 'D': 1},
'B': {'A': 2, 'C': 3, 'D': 2},
'C': {'B': 3, 'D': 3, 'E': 1, 'F': 5},
'D': {'A': 1, 'B': 2, 'C': 3, 'E': 1},
'E': {'C': 1, 'D': 1, 'F': 2},
'F': {'C': 5, 'E': 2}
}
start_node = 'A'
shortest_paths = dijkstra(graph, start_node)
print(shortest_paths)플로이드-워셜(Floyd-Warshall) 알고리즘
플로이드-워셜 알고리즘은 모든 정점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이다. 이 알고리즘은 음의 가중치가 있는 간선이 포함된 그래프에서도 동작하며, 동적 계획법(Dynamic Programming)을 활용한다.
동작 과정:
그래프 초기화: 그래프의 인접 행렬을 초기화한다. 직접 연결된 정점 간의 거리는 해당 간선의 가중치로 설정하고, 연결되지 않은 경우 무한대로 설정한다. 자기 자신으로의 거리는 0으로 설정한다.
경유 정점 고려: 각 정점을 경유지로 설정하여, 두 정점 간의 최단 거리를 갱신한다. 즉, 정점
k를 경유하여i에서j로 가는 경로와 직접 가는 경로를 비교하여 더 짧은 경로를 선택한다.반복: 모든 정점에 대해 위 과정을 반복하여 최단 거리를 갱신한다.
구현 예시
def floyd_warshall(graph):
# 정점의 수
nodes = list(graph.keys())
num_nodes = len(nodes)
# 거리 행렬 초기화
distance = {node: {node: float('inf') for node in nodes} for node in nodes}
for node in nodes:
distance[node][node] = 0
for adjacent, weight in graph[node].items():
distance[node][adjacent] = weight
# 플로이드-워셜 알고리즘
for k in nodes:
for i in nodes:
for j in nodes:
if distance[i][j] > distance[i][k] + distance[k][j]:
distance[i][j] = distance[i][k] + distance[k][j]
return distance구현 예시
graph = {
'A': {'B': 2, 'D': 1},
'B': {'A': 2, 'C': 3, 'D': 2},
'C': {'B': 3, 'D': 3, 'E': 1, 'F': 5},
'D': {'A': 1, 'B': 2, 'C': 3, 'E': 1},
'E': {'C': 1, 'D': 1, 'F': 2},
'F': {'C': 5, 'E': 2}
}
shortest_paths = floyd_warshall(graph)
for start, destinations in shortest_paths.items():
print(f"From {start}:")
for end, distance in destinations.items():
print(f" to {end}: {distance}")결론 및 느낀점
다익스트라(Dijkstra) 알고리즘과 플로이드-워셜(Floyd-Warshall) 알고리즘은 그래프에서 최단 경로를 찾는 데 사용되는 대표적인 알고리즘으로 각 알고리즘의 특징과 사용 시기를 정리하면 아래와 같다.
다익스트라 알고리즘:
- 용도: 단일 시작 정점에서 다른 모든 정점까지의 최단 경로를 구할 때 사용한다.
- 시간 복잡도: 인접 리스트와 우선순위 큐를 사용할 경우 O((V + E) log V)이다.
- 제약 사항: 음의 가중치를 가진 간선이 없는 그래프에서만 동작한다.
- 적용 사례: 네트워크 경로 탐색, GPS 내비게이션 등에서 특정 지점에서 다른 모든 지점까지의 최단 경로를 찾을 때 유용하다.
플로이드-워셜 알고리즘:
- 용도: 모든 정점 쌍 간의 최단 경로를 구할 때 사용한다.
- 시간 복잡도: O(V³)로, 정점의 수가 많을 경우 비효율적일 수 있다.
- 제약 사항: 음의 가중치를 가진 간선을 허용하지만, 음의 사이클이 존재하면 올바르게 동작하지 않는다.
- 적용 사례: 도시 간 최단 경로 계산, 네트워크에서 모든 지점 간의 최단 경로 분석 등에서 활용된다.
알고리즘 선택 전략:
- 그래프의 크기: 정점의 수가 많을 경우, 플로이드-워셜 알고리즘은 시간 복잡도가 높아 비효율적이므로 다익스트라 알고리즘이 더 적합하다.
- 음의 가중치 존재 여부: 그래프에 음의 가중치가 있는 간선이 포함되어 있다면, 다익스트라 알고리즘은 사용할 수 없으므로 플로이드-워셜 알고리즘을 고려해야 한다.
- 필요한 경로의 범위: 단일 출발점에서의 최단 경로만 필요하다면 다익스트라 알고리즘을, 모든 정점 쌍 간의 최단 경로가 필요하다면 플로이드-워셜 알고리즘을 선택하는 것이 좋다.
따라서, 문제의 특성과 요구 사항에 따라 적절한 알고리즘을 선택하여 효율적인 경로 탐색을 수행하는 것이 중요하다.
'Algorithm > 알고리즘' 카테고리의 다른 글
| [암기 필요!] 코딩 테스트 필수 알고리즘 총정리: BFS, DFS, MST, 최단 경로 알고리즘 (0) | 2025.05.28 |
|---|---|
| 3. 백트래킹(Backtracking): 효율적인 완전탐색의 기술 (0) | 2025.05.28 |
| 2. DFS(깊이 우선 탐색): 재귀 함수를 활용한 그래프 탐색 알고리즘의 이해 (0) | 2025.05.28 |
| 1. BFS(너비 우선 탐색): 그래프 탐색 알고리즘의 핵심 이해하기 (0) | 2025.05.28 |
