문제 출처
https://school.programmers.co.kr/learn/courses/30/lessons/72413
문제 설명
밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. "무지"는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. "무지"는 "어피치"와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을 지 계산해 보고 "어피치"에게 합승을 제안해 보려고 합니다.
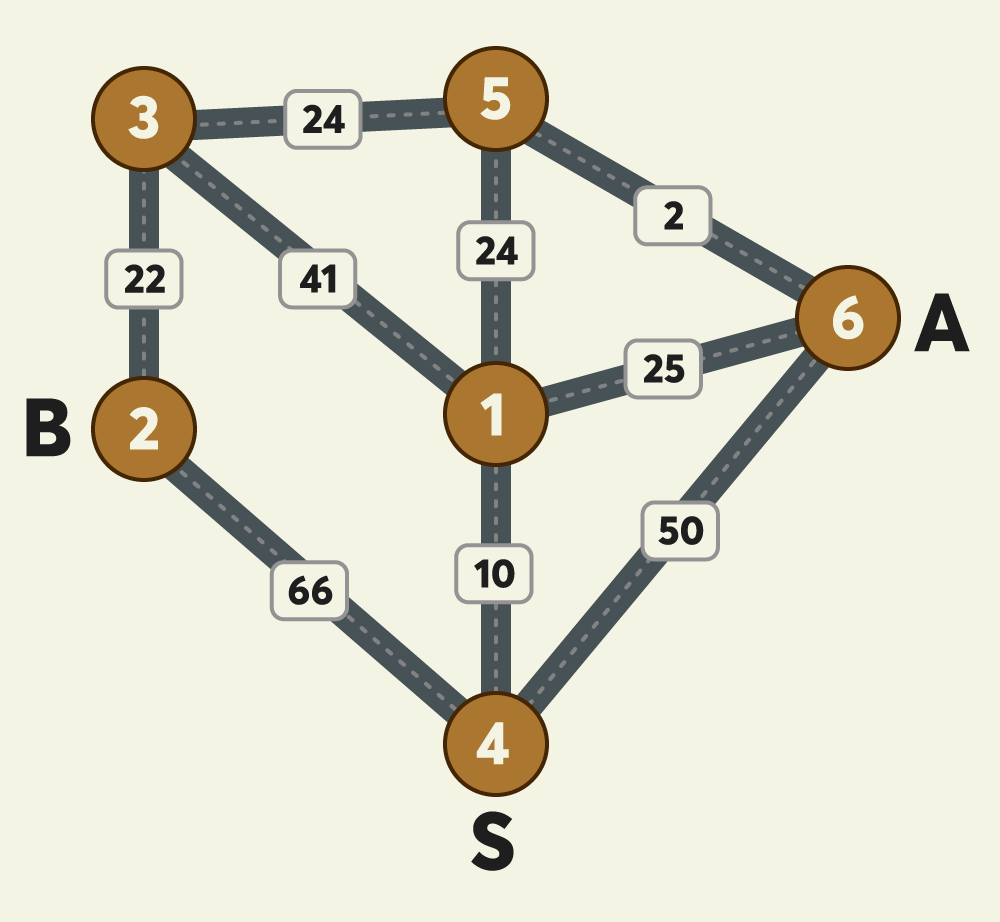
위 예시 그림은 택시가 이동 가능한 반경에 있는 6개 지점 사이의 이동 가능한 택시노선과 예상요금을 보여주고 있습니다.
그림에서 A와 B 두 사람은 출발지점인 4번 지점에서 출발해서 택시를 타고 귀가하려고 합니다. A의 집은 6번 지점에 있으며 B의 집은 2번 지점에 있고 두 사람이 모두 귀가하는 데 소요되는 예상 최저 택시요금이 얼마인 지 계산하려고 합니다.

문제
지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요.
만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 됩니다.
제한사항

내 답안
import math
def solution(n, s, a, b, fares):
INF = math.inf
answer = INF
min_fee = [[INF for _ in range(n)] for _ in range(n)] # 모든 노드 간 초기 비용을 무한대로 설정
# 자기 자신으로 가는 비용은 0으로 설정
for i in range(n):
min_fee[i][i] = 0
# 주어진 간선 정보를 기반으로 초기 비용 설정
for start, end, fee in fares:
min_fee[start - 1][end - 1] = fee
min_fee[end - 1][start - 1] = fee
# 플로이드-워셜 알고리즘 적용
for k in range(n): # 중간 노드
for i in range(n): # 출발 노드
for j in range(n): # 도착 노드
if min_fee[i][j] > min_fee[i][k] + min_fee[k][j]:
min_fee[i][j] = min_fee[i][k] + min_fee[k][j]
# 최소 합승 요금을 계산
for i in range(n):
answer = min(answer, min_fee[s - 1][i] + min_fee[i][a - 1] + min_fee[i][b - 1])
return answer남의 풀이
import heapq
def solution(n, s, a, b, fares):
INF = float('inf')
graph = [[] for _ in range(n + 1)]
# 그래프 초기화
for start, end, cost in fares:
graph[start].append((end, cost))
graph[end].append((start, cost))
# 다익스트라 알고리즘 구현
def dijkstra(start):
distances = [INF] * (n + 1)
distances[start] = 0
queue = [(0, start)] # (거리, 노드)
while queue:
current_dist, current_node = heapq.heappop(queue)
if distances[current_node] < current_dist:
continue
for next_node, weight in graph[current_node]:
distance = current_dist + weight
if distance < distances[next_node]:
distances[next_node] = distance
heapq.heappush(queue, (distance, next_node))
return distances
# 모든 노드에서 출발하는 최단 거리 계산
distances_from_start = dijkstra(s)
distances_from_a = dijkstra(a)
distances_from_b = dijkstra(b)
# 최소 요금 계산
answer = INF
for i in range(1, n + 1):
answer = min(answer, distances_from_start[i] + distances_from_a[i] + distances_from_b[i])
return answer결론 및 느낀점
가장 먼저 생각난 것은 플로이드-워셜 알고리즘을 적용해서 풀면 어떨까였다.플로이드-워셜 알고리즘을 적용하여 코드를 짜서 제출했는데 효율성 테스트에서 아래와 같은 성적표를 받았다.
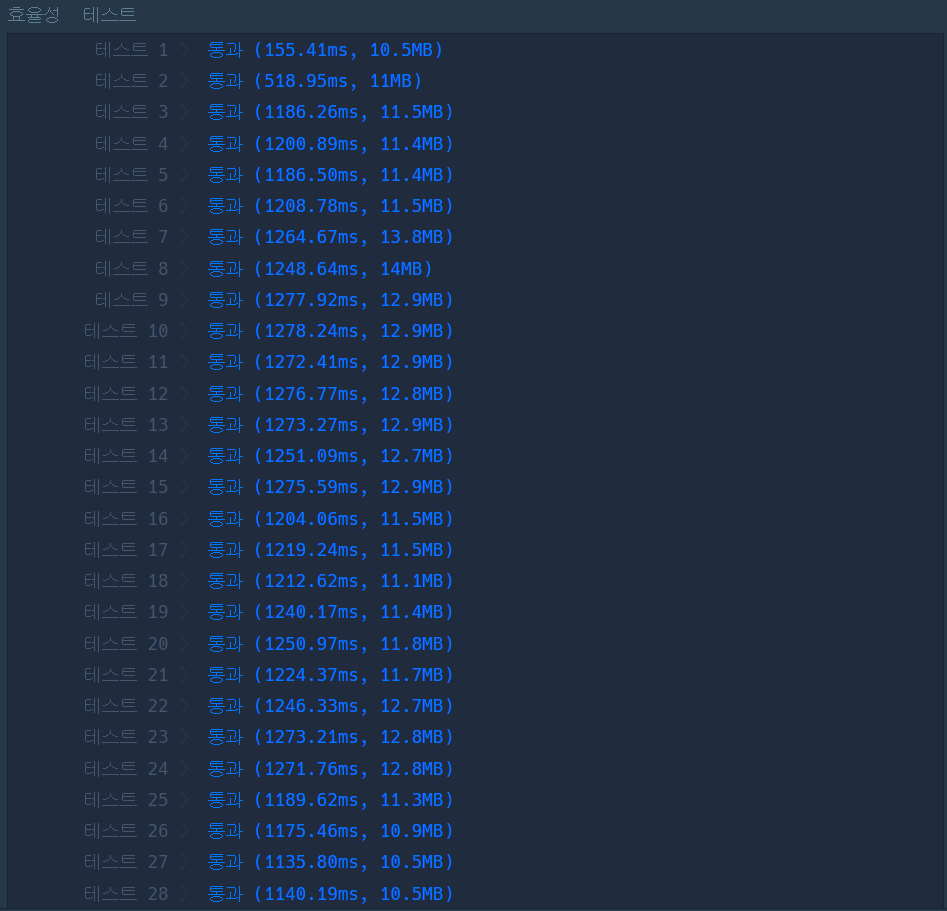
플로이드-워셜 알고리즘은 모든 노드 간의 최단 거리를 계산하기에 구현이 간단하고 직관적이나 시간 복잡도가 O(n^3)이기 때문에 노드 수가 많을 경우 비효율적이었다.
다익스트라 알고리즘은 특정 노드에서 출발하여 다른 노드들로의 최단 거리를 구하는 데 적합한 알고리즘으로 시간 복잡도가 O(ElogV)이기에 노드와 간선의 개수가 많아질수록 효율적이다.
아래는 다익스트라 알고리즘 코드로 돌린 성적표이다.
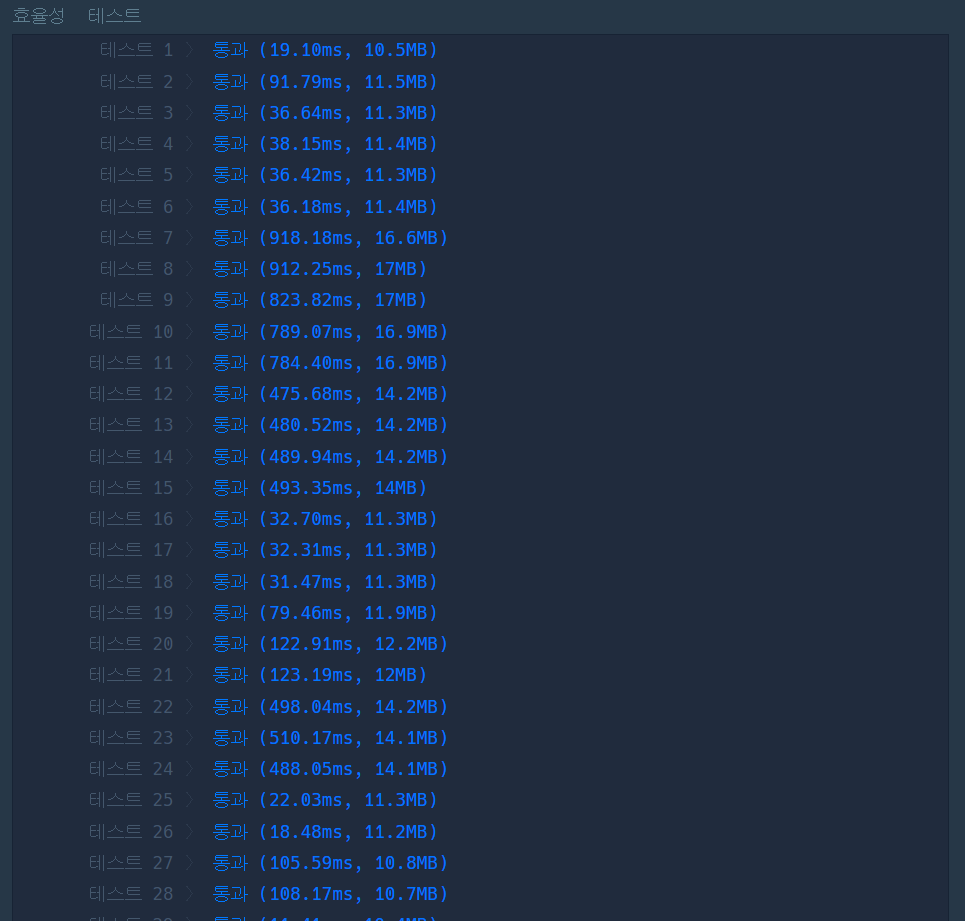
문제에서 주어진 테스트 케이스는 노드의 개수와 간선의 개수가 비교적 많아 다익스트라 알고리즘을 사용하는 것이 효율성 면에서 더 적합했다.
다음에 이와 비슷한 문제가 나와 특정 출발 노드에서 여러 목적지로의 최단 경로를 계산해야 한다면 다익스트라 알고리즘을 우선 고려해봐야겠다.
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스 / PCCP 기출문제 3번 / Python] 충돌위험 찾기 (0) | 2025.05.31 |
|---|---|
| [프로그래머스 / PCCP 기출문제 2번 / Python] 퍼즐 게임 챌린지 (0) | 2025.05.31 |
| [프로그래머스 / PCCP 기출문제 9번 / Python] 지폐 접기 (8) | 2025.05.31 |
| [프로그래머스 / PCCP 기출문제 1번 / Python] 동영상 재생기 (0) | 2025.05.31 |
| [KAKAO BLIND RECRUITMENT / 2023 / Python] 이모티콘 할인행사 (0) | 2025.05.30 |
